二維二骨骼反向動力學解算

▲ Joseph Duffy, "Statics and Kinematics with Applications to Robotics", Cambridge University Press, 1996

Solving Two-Bone IK in 2D
 
　　在上一回NP Lab: Coloring Problem遊戲裡，有兩隻會追蹤玩家滑鼠游標的機械臂。無獨有偶，這兩隻機械臂正好一個是由FK (Forward Kinematics, 正向動力學)控制，而另一個是IK (Inversed Kinematics, 反向動力學)控制。
 
　　正向動力學相對來說簡單很多：由父層級的關節帶動子關節；拿人體來比喻的話就是我先決定上臂的位置(肩關節的角度)，再決定下臂的位置(肘關節的角度)。在遊戲裡，所有的滑鼠位置都可以計算出一個特定的角度值，將上臂移到此位置後，再將下臂直直指向滑鼠，就完成了追蹤。
 
　　反向動力學則剛好相反：由子層級的關節帶動父關節；對於人體來說比較像是伸手去拿茶杯，先知道手要往哪擺，再去想下臂、上臂在哪。而這時候，問題就來了：我們要如何一次求出兩個關節的角度呢？
 
　　接下來這篇文章會帶入IK解算的數學定義、簡述一般通用的算法，並介紹我在NP Lab: Coloring Problem中所用的簡化算法。
 

一、問題定義
 
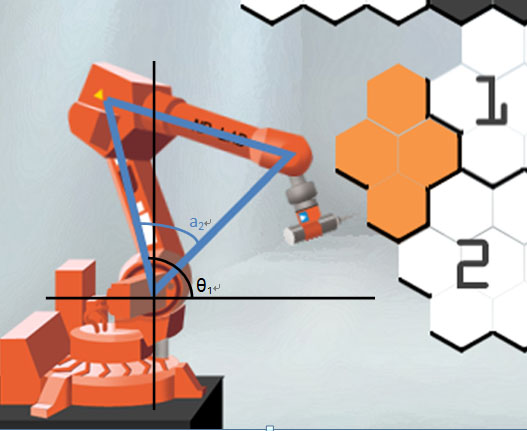
　　給定一個骨骼Bone₁與Bone₂構成的骨骼鏈，其中Bone₁位於原點O，Bone₂為Bone₁的子骨骼，且每個骨骼均具有角度θ與固定的長度參數d (如下圖一)。請問：給定一點T(x, y)，θ₁與θ₂各要是多少，才能使Bone₂的尾端恰好位於T點？
 

▲圖一

二、可解範圍
 
　　不論是 d₁ < d₂ (如下圖二)或是 d₁ > d₂ (圖三)的情況，假如我們使θ₁固定為0 (Bone₁與x軸重疊)，則此骨骼系統所能夠碰觸到的點只有圖中綠圈線上的所有點而已。此時旋轉Bone₁，我們可以很清楚的看到，此二骨骼系統所能搆到的最遠距離就是d₁ + d₂，而在離原點距離小於 | d₁ - d₂ | 的點會處於死角之中搆不到。

▲圖二、圖三

 
　　換言之，T與原點的距離關係必須符合下列式子，否則此骨骼系統無法達到「使Bone₂的尾端恰好位於T點」的目標：
 

| d₁ - d₂ | ≦ OT ≦ (d₁ + d₂)

 
三、解算
 
　　一般用到IK控制的場合中，考慮到關節角度限制、以及為了方便推廣到多骨骼的場合，一般會如圖四分解問題：

▲圖四

 
　　在這個架構下，求解θ₁、θ₂，其實就是在解下列的聯立方程：
 

x = d₁ cos θ₁ + d₂ cos(θ₁ + θ₂)

y = d₁ sin θ₁ + d₂ sin(θ₁ + θ₂)

 
　　此式雖可化簡，但過程繁瑣，在此不詳列。
 
　　在NP Lab: Coloring Problem中，由於關節沒有角度限制，且所有滑鼠座標均事先映射到可解範圍之中，所以我就用了一個相對簡單的算法來作IK解算。
 
 
四、利用餘弦定理
 
　　我們把圖一重新畫上輔助線如下圖五，其中d₃ = | OT | ，θ₁ = (OT與x軸夾角 - a₂)，θ₂ = (180˚ - a₃)。

▲圖五

 
　　在d1、d2、d3均為已知的情況，整個問題就變成了「已知三邊長，求角度」的形式。只要利用餘弦定理即可解出：
 

a₁ = cos^-1( (d₂² + d₃² - d₁²) / 2d₂d₃ )

a₂ = cos^-1( (d₁² + d₃² - d₂²) / 2d₁d₃ )

a₃ = cos^-1( (d₁² + d₂² - d₃²) / 2d₁d₂ )

 
　　要注意的是，這裡求出來的數值是角度而不是角向量，所以角度的加減要考慮進去。例如底下圖六就是一個不同的狀況：θ₁ = (OT與x軸夾角 + a₂)
 

▲圖六

五、小結
 
　　IK控制在2D遊戲中其實並不多見，主要用在「需要適應環境」的情境中，例如沙羅曼蛇的觸手魔王就是一個很好的例子。3D環境中IK控制就用得多了，要讓雙腳踏在斜坡上不會一腳踏空一腳插進地表時可以用來修正膝蓋、股關節的角度，跳躍、攀爬的誤差也可以依同法修正，用途廣泛。不過......這就留給之後再來研究吧！ XD